لمحة عن المقال
تُعد المعادلات التربيعية من المفاهيم الأساسية التي يتعلمها التلاميذ في التعليم الأساسي، وخاصة في مراحل الصفوف المتوسطة، وعادةً ما تبدأ في الظهور بشكلٍ أوضح للطلاب الذين تتراوح أعمارهم بين 12 و15 سنة. المعادلة التربيعية هي معادلة جبرية تكون بصيغة عامة على الشكل التالي:
ax² + bx + c = 0
حيث أن a وb وc هي أعداد حقيقية، وa ≠ 0. إذا كان الحد a يساوي صفرًا، فإن المعادلة تصبح خطية وليست تربيعية. تُستخدم المعادلات التربيعية في العديد من التطبيقات العملية، مثل فيزياء الحركة، الاقتصاد، والهندسة المعمارية. في هذا المقال، سنتناول كيفية استخدام صيغة المعادلة التربيعية للحل، مع شرح مفصل ومناسب لمستوى طلاب المدارس، كما سنعرض تطبيقات حياتية تساعد على فهم أهمية هذا الموضوع.
ما هي صيغة المعادلة التربيعية؟
لحل أي معادلة تربيعية، يمكن استخدام الصيغة التربيعية (Quadratic Formula) والتي تُستخدم لإيجاد جذور المعادلة أو القيم التي تجعل المعادلة تساوي صفرًا. الصيغة هي:
x = (-b ± √(b² – 4ac)) / (2a)
هذه الصيغة تستخرج قيم x وهي المجهول أو المجهولين في المعادلة. تتضمن الصيغة ثلاثة معاملات هي a وb وc مأخوذة مباشرة من المعادلة.:
- a: معامل x²
- b: معامل x
- c: الحد الثابت
ولكي تستخدم هذه الصيغة، يجب أن تتأكد أولاً من أن المعادلة مكتوبة بالصورة القياسية، أي بها الحدود الثلاثة بالترتيب: مربع المجهول، ثم المجهول، ثم العدد.
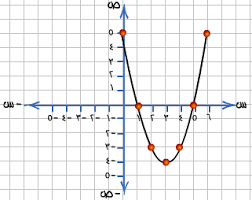
شرح عناصر الصيغة التربيعية
يرتكز حل المعادلة التربيعية باستخدام الصيغة على فهم جزء مهم منها يُعرف بـ المميز أو Discriminant، وهو الجزء الموجود أسفل الجذر التربيعي:
D = b² – 4ac
يُستخدم المميز لتحديد نوع جذور المعادلة، سواء كانت:
- D > 0: وجود حلين حقيقيين ومختلفين.
- D = 0: وجود حل حقيقي واحد (الجذران متساويان).
- D < 0: لا توجد حلول حقيقية، وإنما حلول مركبة (عادة تدرس في مستويات دراسية أعلى).
من خلال فهم قيمة المميز، يمكن للطالب معرفة نوع الجذور دون القيام بعملية الجذر التربيعي فعليًا، مما يسهل عليه التحليل المسبق.
مثال تطبيقي على استخدام الصيغة
المثال:
حل المعادلة: 2x² + 3x – 2 = 0
الحل:
- a = 2
- b = 3
- c = -2
نحسب المميز أولاً:
D = b² – 4ac = 3² – 4 × 2 × (-2) = 9 + 16 = 25
بما أن D > 0، فلدينا حلين حقيقيين مختلفين. نستخدم الصيغة:
x = (-3 ± √25) / (2 × 2)
x = (-3 ± 5) / 4
نحسب الجذرين:
- x₁ = (-3 + 5) / 4 = 2 / 4 = 0.5
- x₂ = (-3 – 5) / 4 = -8 / 4 = -2
إذاً، جذرا المعادلة هما x = 0.5 وx = -2.
أهمية فهم الصيغة التربيعية في الحياة اليومية
ليست صيغة المعادلة التربيعية مجرد خطوة تعليمية، بل هي أداة مفيدة لحل مشكلات حقيقية في الحياة. في مجالات مثل حساب المسافات في الفيزياء أو تكاليف الإنتاج في الاقتصاد أو حتى تصميم المباني في الهندسة المعمارية، يتم استخدام هذه الصيغة للحصول على الحلول الأنسب.
في كرة القدم، عندما يرمي اللاعب الكرة في قوس عالٍ نحو المرمى،ُ تكون حركة الكرة على شكل قطع مكافئ، ويمكن تمثيل مسارها بواسطة معادلة تربيعية. لذا فإن استخدام الصيغة التربيعية يسمح بحساب الزاوية المناسبة لضمان دخول الكرة في المرمى.
هذا المثال الواقعي يوضح كيف أن الفهم الجيد للرياضيات يساعد في تحليل الظواهر التي نراها يوميًا، ويمكّننا من الاقتراب أكثر من العالم الحقيقي من حولنا.
أخطاء شائعة يجب تجنبها
عند استخدام صيغة المعادلة التربيعية، هناك عدة أخطاء شائعة قد يقع فيها الطلاب، ومن أهمها:
- نسيان إشارة السالب أمام b في الصيغة. تذكر أن الصيغة تبدأ بـ -b وليس فقط b.
- حساب خاطئ لقيمة b² أو لعملية الضرب 4ac، لذلك يجب التأكد من العمليات الحسابية.
- نسيان أن المقام هو 2a، وليس فقط 2.
- عدم استخراج الجذر التربيعي لقيمة المميز √D بشكل صحيح، خصوصًا إذا لم تكن القيمة مربعة تمامًا.
لفهم هذا جيدًا، ينصح بممارسة الأمثلة تدريجياً، والبدء بأمثلة تحتوي على جذور كاملة مثل √4 أو √9، قبل التدرج إلى جذور غير تامة.
متى تُستخدم الصيغة التربيعية؟
ليست كل المعادلات التربيعية تحتاج لصيغة المعادلة التربيعية لحلها. في بعض الحالات، تكون المعادلة قابلة للتحليل (مثل استخدام طريقة الفرق بين مربعين أو إكمال المربع). لكن إذا كانت المعادلة لا تُحل بسهولة بتلك الطرق، فإن استخدام الصيغة يكون هو الحل الأفضل والدقيق.
كذلك في حالات الاختبارات أو التطبيقات الحاسوبية، تُعتبر الصيغة التربيعية هي الأكثر كفاءة لحل المعادلات التربيعية المنهجية وبأقل احتمال للخطأ.
نصائح لتعلم الصيغة بسهولة
لتسهيل حفظ وتطبيق الصيغة التربيعية، يمكن اتباع النصائح التالية:
- كتابة الصيغة أكثر من مرة حتى يتم حفظها عن ظهر قلب.
- رسم مخطط أو صورة توضيحية تشير إلى مواقع a وb وc في المعادلة الأصلية.
- التدرب على حالات مختلفة (مثل أن يكون المميز موجبا، صفرا أو سالبا).
- استخدام الألوان لتحديد الأجزاء المختلفة في المعادلة والصيغة.
كل هذه الوسائل تساعد على ترسيخ المفهوم بصريًا وذهنيًا، خاصة للأطفال الذين يعتمدون على التعلم من خلال الصور والتمثيل البصري.
تطبيقات وتمارين إضافية
لفهم الموضوع جيدًا، ننصح بالقيام بالعديد من التمارين العملية، مثل:
- حل المعادلة x² – 6x + 9 = 0 باستخدام الصيغة.
- حل المعادلة 3x² + 2x – 8 = 0.
- إيجاد نوع الجذور فقط دون الحل، مثلًا للمعادلة 5x² – 4x + 1 = 0 باستخدام حساب قيمة المميز فقط.
كل تمرين من هذه التمارين يساعد الطالب على التمرس في صيغة حل المعادلة التربيعية، وتوسيع قدرته على التعمق فيها.
الربط مع مواد أخرى
يمكن ربط المعادلة التربيعية بأكثر من مادة دراسية:
- العلوم: في دروس الحركة والجاذبية الأرضية.
- الجغرافيا: في حساب المساحات الجغرافية التي تحتوي على تعرجات أو ميل.
- التربية الفنية: في رسم الأقواس والقطع المكافئ بدقة هندسية.
مثل هذه الروابط تخلق بيئة تعلم تكاملية تشجع الطالب على فهم أهمية ما يتعلمه في الرياضيات.
صيغة المعادلة التربيعية هي أداة قوية تمكّن الطالب من حل جميع المعادلات من الدرجة الثانية بطريقة منظمة وواضحة. إنها ليست مجرد قاعدة رياضية، بل وسيلة لحل مشكلات من الواقع والتفكير المنطقي والتخطيط. فكلما تمكّن الطالب من فهم تلك الصيغة واستيعاب عناصرها المختلفة وطريقة استخدامها، أصبح أكثر قدرة على التعامل مع مسائل معقدة، مما يؤدي إلى تنمية قدراته التحليلية والإبداعية.






