لمحة عن المقال
الخط المستقيم هو أحد المفاهيم الأساسية في الرياضيات والهندسة، ويُقصد به المسار الذي يمتد في اتجاه واحد دون انحناء أو بداية أو نهاية. يُستخدم الخط المستقيم كثيرًا في دراسة الإحداثيات والمواقف الحياتية اليومية، مثل الطرق المستقيمة، حواف الأبنية، وغيرها من الأمثلة التي تظهر في الطبيعة والهندسة. يُعد الخط المستقيم أداة هامة لفهم العلاقات بين المتغيرات في الرياضيات وتطبيقاتها في العالم الواقعي.
المفهوم العام لمعادلة الخط المستقيم
عندما نرسم خطًا مستقيمًا في المستوى الإحداثي (والذي يتكوّن من محور أفقي يُسمى المحور السيني x ومحور عمودي يُسمى المحور الصادي y)، فإن كل نقطة على هذا الخط لها قيم محددة لـ x و y. معادلة الخط المستقيم هي علاقة رياضية تمثّل جميع تلك النقاط التي تقع على نفس الخط. بمجرّد أن نعرف معادلة الخط، فإننا نستطيع رسمه وتوقّع أين توجد نقاط جديدة عليه دون الحاجة إلى رسمها يدويًا.
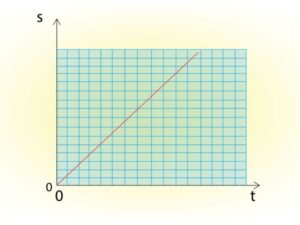
الصيغة الأساسية لمعادلة الخط المستقيم
الصيغة الأكثر شيوعًا لمعادلة الخط المستقيم هي:
y = mx + b
حيث:
- y هو الإحداثي العمودي للنقطة.
- x هو الإحداثي الأفقي للنقطة.
- m هو الميل (أو انحدار الخط)، وهو يحدد مدى انحدار الخط نحو الأعلى أو الأسفل.
- b هو التقاطع مع محور y، أي النقطة التي يقطع فيها الخط المحور الصادي عندما تكون x = 0.
من خلال هذه المعادلة، نستطيع إنشاء أي خط مستقيم عن طريق تحديد قيمة الميل والتقاطع مع المحور الصادي.
ما هو الميل؟
الميل هو الجزء الأهم في معادلة الخط المستقيم، وهو يدل على مدى انحدار الخط، سواء كان صاعدًا من اليسار إلى اليمين (إذا كان الميل موجبًا)، أو نازلًا (إذا كان الميل سالبًا). ويحسب الميل بواسطة العلاقة التالية:
m = (فرق الصادات) / (فرق السينات) = (y₂ – y₁) / (x₂ – x₁)
بمعنى نحن نأخذ نقطتين من الخط، نحسب الفرق بين إحداثياتها العمودية (الصادية)، ثم نقسمه على الفرق بين الإحداثيات الأفقية (السينية). كلما كانت النسبة أكبر، فإن الخط يكون أكثر انحدارًا.
أمثلة على حساب الميل
إذا أعطينا نقطتين مثلاً (1, 2) و (3, 6)، فإن حساب الميل يكون:
m = (6 – 2) / (3 – 1) = 4 / 2 = 2
هذا يعني أن كلما تقدمنا خطوتين على محور x، نرتفع خطوتين على محور y، وبالتالي الخط صاعد بانتظام.
ما هو التقاطع مع المحور الصادي؟
عندما نكتب معادلة الخط المستقيم على شكل y = mx + b، فإن b تمثل النقطة التي يقطع فيها الخط المحور y عندما تكون x = 0. هذه النقطة مهمة؛ لأنها تُظهر أين يبدأ الخط إذا كنا نرسمه من جهة اليسار على الرسم البياني.
مثلاً، إذا كانت لدينا المعادلة:
y = 3x + 1
فإن هذا يعني أن الخط يبدأ من النقطة (0, 1) ويصعد بمعدل 3 وحدات صعود لكل وحدة أفقية واحدة.
أشكال أخرى من معادلة الخط المستقيم
رغم أن الصيغة العامة y = mx + b هي الأكثر استخدامًا، إلا أن هناك صورًا أخرى يمكن من خلالها كتابة معادلة الخط المستقيم، وهذه الصور تُستخدم في حالات معينة أو لتسهيل بعض العمليات.
١- صيغة الميل والنقطة
عندما نعرف نقطة واحدة على الخط وميله، فنستخدم صيغة “الميل والنقطة”:
y – y₁ = m(x – x₁)
حيث (x₁, y₁) هي نقطة معلومة على الخط، وm هو الميل. هذه الصيغة مفيدة عندما لا نعرف إلا نقطة واحدة على الخط مع ميله.
٢- الصيغة العامة للخط المستقيم
تُكتب على الشكل:
Ax + By + C = 0
وهي صيغة عامة تُستخدم في الدراسة المتقدمة لبعض خصائص الخطوط مثل التوازي والتعامد. إلا أن هذه الصيغة أقل استخدامًا في المرحلة الابتدائية.
كيف نرسم الخط المستقيم من خلال معادلته؟
لرسم الخط المستقيم من المعادلة، نتبع بعض الخطوات البسيطة:
- نبدأ بحساب أو تحديد النقطة التي يقطع فيها الخط المحور الصادي (b).
- نستخدم الميل (m) لتحريك النقطة الأولى ورسم النقطة التالية. إذا كان الميل 2، فإننا نصعد وحدتين وننتقل وحدة واحدة إلى اليمين على المحور x.
- نربط بين النقطتين بخط مستقيم ويمكننا تكرار العملية لإنشاء أكثر من نقطة.
هل تعلم أن المهندسين يستخدمون معادلة الخط المستقيم لتحديد ميل الطرق؟ فإذا كان الطريق مائلًا جدًا، يكون من الصعب على السيارات الصعود، لذا لابد من دراسة معادلة الخط حتى تكون الانحدارات آمنة!
أمثلة من الحياة اليومية
معادلة الخط المستقيم لا تستخدم فقط داخل فصول الرياضيات بل توجد حولنا في الحياة. فمثلاً:
- إذا كنت توفر مقدارًا ثابتًا من المال شهريًا، فالعلاقة بين الشهر والمبلغ المدّخر تكون على شكل خط مستقيم.
- عند حساب تكلفة شراء عدد معين من المنتجات، إذا كانت كل واحدة بسعر ثابت، فإن مجموع السعر مع عدد المنتجات يمثّل خطًا مستقيمًا.
- في مواقف السيارات التي تتقاضى رسومًا ثابتة لكل ساعة، فإن العلاقة بين عدد الساعات والتكلفة تكون على شكل خط مستقيم.
التمييز بين أنواع الخطوط حسب الميل
يمكن تمييز الخطوط المختلفة على أساس قيمة الميل:
- الميل الموجب: الخط صاعد من اليسار إلى اليمين.
- الميل السالب: الخط نازل من اليسار إلى اليمين.
- الميل صفر: الخط مستقيم أفقي لا يصعد ولا ينزل.
- الميل غير معرّف: الخط عمودي، أي في اتجاه الأعلى والأسفل، ولا يمكن معادلة ميله.
التوازي والتعامد بين الخطوط باستخدام الميل
إذا كان لدينا خطان ونريد معرفة إن كانا متوازيين أو متعامدين، فإن الميل يساعدنا على ذلك:
- الخطان يكونان متوازيَيْن إذا كان لهما نفس الميل تمامًا.
- الخطان يكونان متعامدين إذا كان حاصل ضرب ميليهما يساوي -1.
هذه القواعد تساعد في حل كثير من المسائل الهندسية لا سيّما في الرسم والتصميم.
تطبيقات معادلة الخط المستقيم في المراحل الابتدائية
رغم أن المواضيع يبدو أنها رياضيات متقدمة، إلا أن أطفال المرحلة الابتدائية يمكنهم فهم معادلة الخط المستقيم بسهولة عن طريق اللعب، الرسم، وتجربيها عمليًا. مثلًا، يمكن للأطفال تحديد سعر منتج واحد، ثم جدولة الأسعار عند شراء 2، 3، 4 … منتج. سيتبيّن لهم أن العلاقة بينها خط مستقيم، ويمكن رسمه على ورق بياني.
تُستخدم معادلة الخط أيضًا في الأنشطة التي تشمل البيانات، مثل درجة حرارة اليوم خلال ساعات النهار، أو عدد الكتب المقروءة خلال عدة أيام. وتُستخدم حتى في برامج الكمبيوتر والألعاب الإلكترونية لتحديد حركات الكائنات.
نصائح لتعلّم وفهم معادلة الخط المستقيم
لتعلّم معادلة الخط المستقيم بشكل أفضل، إليكم بعض النصائح:
- ابدأ بفهم الرسم البياني وتعرّف على المحاور.
- تمرّن على تحديد النقاط ورسمها على المستوى الإحداثي.
- تعلم كيف تحسب الميل من نقطتين، وثم استخدمه في المعادلة.
- قم بإنشاء معادلات لخطوط مختلفة وجرّب رسمها.
- لاحظ الفرق بين ميل الخطوط المختلفة، وماذا يعطي كل منها من شكل أو اتجاه.
مشكلات محلولة باستخدام معادلة الخط
مثال 1: ما معادلة الخط المستقيم الذي ميله 2 ويقطع المحور الصادي عند النقطة (0, -3)؟
نُطبّق المعادلة: y = mx + b
فنجد أن y = 2x – 3
مثال 2: ما هو الميل إذا كان لدينا نقطتين: (2, 4) و (4, 10)؟
m = (10 – 4) / (4 – 2) = 6 / 2 = 3
مثال 3: ما معادلة الخط المارّ بالنقطة (1, 2) وميله -1؟
نستخدم صيغة الميل والنقطة:
y – 2 = -1(x – 1) ← y = -x + 3






