لمحة عن المقال
تُعد الخطوط من المفاهيم الأساسية في علم الهندسة التحليلية، وهي تُستخدم لفهم العلاقات والمواقع في المستوى الإحداثي. يُعرف الخط المستقيم في الهندسة التحليلية على أنه مجموعة من النقاط التي تقع في نفس المسار وتتبع قاعدة رياضية معينة. وعادة ما يُمثل الخط باستخدام معادلة من الشكل ص = مx + جـ، حيث م هو الميل وجـ هو الجزء المقطوع من محور الصادات. من خلال دراسة الخطوط، يمكن للطلاب التعرف على العلاقات المكانية مثل التوازي والتعامد، والتي تعتبر من المفاهيم الأساسية في تعليم الرياضيات من المرحلة الابتدائية حتى الثانوية.
الخطوط المتوازية
الخطوط المتوازية هي خطوط لا تلتقي أبدًا، مهما امتدت في الفضاء ثنائي الأبعاد. وهذا يعني أنها تحتفظ بنفس المسافة بين بعضها البعض في جميع الأحيان. من الناحية التحليلية، يمكن تمييز الخطوط المتوازية من خلال ميلها. فإذا كان لدينا خطين مستقيمين لهما نفس الميل (م1 = م2) لكن لهما معاملات جـ مختلفة، فإن هذين الخطين يكونان متوازيين.
على سبيل المثال، الخطين الذين معادلتيهما:
ص = 2س + 3 و ص = 2س – 5
هما خطين متوازيين لأن لهما نفس الميل وهو 2، ولكن مختلفين في الجزء المقطوع من محور الصادات (3 و -5).
في المستوى المدرسي، يمكن اعتبار هذا المفهوم بداية لفهم أكثر تعقيداً في الرياضيات مثل الرسومات البيانية وتحليل الحركات والنماذج الرياضية في العلم والهندسة.
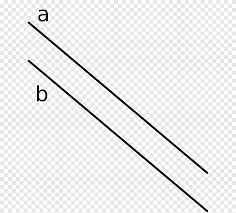
خصائص الخطوط المتوازية
- لها نفس الميل.
- لا تلتقي أبداً، أي لا يوجد لهما نقطة تقاطع.
- المسافة بين أي نقطتين من الخطين المتوازيين تظل ثابتة.
أمثلة على استخدام الخطوط المتوازية
الخطوط المتوازية تُستخدم في تصميم الطرق والسكك الحديدية، والهندسة المعمارية، والرسم الهندسي، حيث من المهم الحفاظ على توازي عناصر البناء لضمان الثبات والدقة.
في السكك الحديدية، توضع القضبان على مسافات ثابتة ومتوازية بدقة لضمان حركة القطار بسلاسة وأمان. هذا التوازي يحافظ على استقرار القطار أثناء السير بسرعات عالية.
الخطوط المتعامدة
الخطوط المتعامدة هي خطوط تتقاطع في نقطة واحدة وتشكل زاوية قائمة (90 درجة). في الهندسة التحليلية، إذا كان هناك خطين، وكان حاصل ضرب ميلهما يساوي -1 أي (م1 × م2 = -1)، فإن الخطين يكونان متعامدين.
مثال على ذلك:
إذا كان عندنا خطين:
ص = 3س + 1، فإن ميله هو 3.
فلكي يكون هناك خط آخر متعامد معه، يجب أن يكون ميله -1/3 لأن: 3 × -1/3 = -1.
إذن معادلة الخط المتعامد معه قد تكون: ص = -1/3س + 2
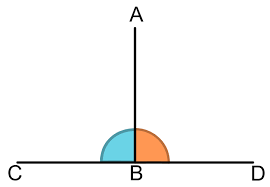
خصائص الخطوط المتعامدة
- تتقاطع في نقطة واحدة فقط.
- تشكل زاوية قائمة بمقدار 90 درجة.
- حاصل ضرب ميليهما يساوي -1.
أمثلة على استخدام الخطوط المتعامدة
الخطوط المتعامدة تظهر في معظم الأبنية والمنشآت. فالجدران تكون عادة متعامدة مع الأرض لضمان الاستقامة والتوازن. كما تُستخدم الخطوط المتعامدة في تخطيط المدن والشوارع لتسهيل حركة السيارات والمشاة.
عند تصميم إشارات المرور والتقاطعات، يتم استخدام مفهوم الخطوط المتعامدة لضمان أن التقاطع بين الطرق يشكل زوايا قائمة، ما يسمح برؤية واضحة وتقسيم فعال للمساحات.
الميل والعلاقة بين الخطوط
الميل هو نسبة التغير في الإحداثي y إلى التغير في الإحداثي x بين أي نقطتين على الخط. ويحسب باستخدام الصيغة:
م = (ص2 – ص1)/(س2 – س1)
وهذا الميل هو المفتاح لتحديد ما إذا كانت الخطوط متوازية أو متعامدة. فعندما يكون الميلان متساويين، يكون الخطان متوازيين، وعندما يكون حاصل ضرب الميلين -1، يكون الخطان متعامدين.
في المرحلة الأساسية والإعدادية، يساعد تدريب الطلاب على حساب الميل من خلال نقاط معينة على فهم العلاقة بين الخطوط، وهو ما يُعد جاهزية لمرحلة الرسوم البيانية في المرحلة الثانوية.
التحقق من التوازي والتعامد باستخدام النقاط
في بعض التمارين، يُطلب من الطالب تحديد ما إذا كانت الخطوط التي تمر من خلال نقطتين متوازية أو متعامدة. في هذه الحالة، يُحسب الميل بين كل زوج من النقطتين ويُقارن الميلان.
مثال:
النقطتين A(1, 2) و B(3, 6) والنقطتين C(0, 4) و D(2, 8).
ميل AB = (6 – 2)/(3 – 1) = 4/2 = 2
ميل CD = (8 – 4)/(2 – 0) = 4/2 = 2
وبما أن الميلان متساويان، فإن الخط المستقيم AB توازي الخط المستقيم CD.
التطبيقات التعليمية
في الصفوف الابتدائية، يُمكن للمعلمين استخدام رسومات وأمثلة بصرية لتوضيح مفهومي التوازي والتعامد. وغالباً ما يُستخدم المربعات والمثلثات والمستطيلات كنماذج بسيطة لتوضيح العلاقات بين الخطوط. كما يمكن للطلاب قياس الزوايا باستخدام منقلة للتأكد أن الخطين يشكلان زاوية قائمة في حالة التعامد.
أما في المراحل الإعدادية والثانوية، فتصبح الحسابات أكثر عمقًا باستخدام الإحداثيات، والرسوم البيانية، والمعادلات. ويمكن توسيع المفهوم ليشمل حل أنظمة من المعادلات، وتحليل خصائص الدوال الخطية.
العلاقة بين التوازي والتعامد في الأشكال الهندسية
العديد من الأشكال الهندسية تعتمد على المفهومين معًا. فمثلاً:
- المربع: جميع أضلاعه متساوية، وكل ضلعين متقابلين متوازيين، وكل زاويتين متلاقيتين بين الضلوع متعامدتين.
- المستطيل: له أربعة أضلاع، كل ضلعين متقابلين متوازيين، وزواياه قائمة، أي أن أضلاعه تتعامد.
- المعين والمعشقات الهندسية: تستخدم توازي وتقاطع الخطوط بشكل يوضح التفاعل بين المفهومين.
فهم العلاقات بين الخطوط داخل هذه الأشكال يساعد الطالب على التفكير التحليلي وتطبيق المهارات المكتسبة من الهندسة التحليلية في مسائل أكثر تعقيداً في الهندسة المستوية أو الصلبة.
استخدام البرمجيات والأدوات التفاعلية
تشجع الكثير من المناهج التعليمية الحديثة على استخدام التكنولوجيا لتدريس المفاهيم الرياضية. ففي موضوع مثل الخطوط المتوازية والمتعامدة، يمكن استخدام برمجيات مثل GeoGebra أو Desmos لعرض الرسوم البيانية، والتجريب مع ميل الخطوط، وملاحظة التوازي أو التعامد عبر التعديل المباشر للمعادلات والنقاط.
كما يمكن للطلاب رؤية العلاقة التفاعلية بين الميل والتوازي أو التعامد لتقوية الفهم البصري والتجريبي للمحتوى. كذلك، يحمل هذا الأسلوب فرصاً لذوي صعوبات التعلم ومحبي الاستكشاف العملي.
أهمية تدريس المفهوم
يُعتبر فهم الخطوط المتوازية والمتعامدة من الركائز الأساسية في بناء التفكير الهندسي والمنطقي عند الطلاب. فهو يساعدهم في:
- التمييز بين العلاقات الهندسية البسيطة والمعقدة.
- بناء نماذج رياضية للمشكلات الواقعية.
- فهم البُعد المكاني والتناظر.
- التطبيق في العلوم الأخرى مثل الفيزياء عند تحليل الحركات والقوى.
ولذلك، يُعد هذا المفهوم أحد المداخل المهمة للتقدم في مجالات الهندسة، العمارة، التصميم، وحتى الذكاء الاصطناعي وتحليل البيانات في مرحلته المتقدمة.






