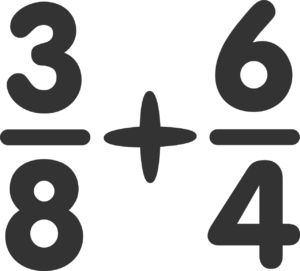يُعتبر فهم الكسور من المهارات الرياضية الأساسية التي يتعلمها الطلاب في المرحلة الابتدائية، ويُعد جمع الأعداد الكسرية من أهم العمليات التي تعزز القدرة الحسابية وتُستخدم في الحياة اليومية، مثل قياس الأطوال أو تقسيم الطعام أو إدارة الوقت. في هذا المقال، سنتناول شرحًا كاملاً لمفهوم جمع الأعداد الكسرية، وأهم القواعد اللازمة لإجراء هذه العمليات الحسابية بالشكل الصحيح، مع تقديم أمثلة عملية وتمارين تطبيقية لتسهيل الفهم، وكل ذلك بلغة بسيطة موجهة خصيصًا لطلاب المرحلة الابتدائية الذين تتراوح أعمارهم بين 7 و15 سنة.
ما هو العدد الكسري؟
العدد الكسري هو عدد يُعبّر عن جزء من كل. وعادةً ما يُكتب العدد الكسري على صورة “بسط/مقام”. فمثلاً، الكسر ¾ يعني ثلاثة أجزاء من أربعة أجزاء متساوية. إذا كان عندنا بيتزا مقسومة إلى أربعة أجزاء وأخذنا منها ثلاثة، فإننا نكون قد أخذنا ¾ من البيتزا. البسط هو الرقم العلوي في الكسر ويدل على عدد الأجزاء المأخوذة، بينما المقام هو الرقم السفلي ويدل على عدد الأجزاء الكلية التي تم تقسيم الشيء إليها.
أنواع الأعداد الكسرية
تنقسم الأعداد الكسرية إلى نوعين رئيسيين:
1. الكسور العادية
هي الأعداد التي تكتب على صورة “بسط/مقام”، مثل ½ أو ¾ أو 5/8. هذه الكسور تصف جزءًا من كمية معينة.
2. الكسور غير الحقيقية (الأعداد الكسرية أو الكسور المركبة)
وهي الكسور التي يكون فيها البسط أكبر من المقام، مثل 7/4 أو 9/2. يمكن أيضًا تحويل هذه الكسور إلى صورة عدد كسري مكوّن من عدد صحيح وكسر، مثل 7/4 = 1 ¾.
متى نحتاج إلى جمع الأعداد الكسرية؟
نحتاج إلى جمع الأعداد الكسرية في كثير من مواقف الحياة. على سبيل المثال، إذا شرب طالب في اليوم الأول ⅔ لتر من الحليب، وفي اليوم الثاني شرب ¾ لتر آخر، ويريد معرفة الكمية التي شربها خلال اليومين، فإنه سيحتاج إلى جمع الكسرين. وبذلك، تُعد مهارة جمع الكسور ضرورية لفهم كميات متعددة أو إجراء قياسات دقيقة.
معلومة رياضية: في الطهي والمخبوزات، عادة ما تُستعمل الكسور لجمع كميات من المكونات. فمثلًا، إذا وضعت ½ كوب من السكر في خليط الكيك ثم أضفت ⅓ كوب آخر، تحتاج إلى جمع الكسور (½ + ⅓ = 5/6 كوب) لضبط كمية المكونات بدقة!
خطوات جمع الأعداد الكسرية
لجمع الأعداد الكسرية بشكل صحيح، هناك خطوات محددة يجب اتباعها. وهذه الخطوات تختلف قليلاً باختلاف نوع الكسر الذي نريد جمعه. فيما يلي الخطوات التفصيلية:
الحالة الأولى: جمع كسور ذات نفس المقام
عندما يكون الكسران المراد جمعهما لهما المقام نفسه، تكون عملية الجمع سهلة ومباشرة. فقط نقوم بجمع البسطين ويبقى المقام كما هو.
مثال: ⅓ + ⅓ = (1 + 1)/3 = 2/3
مثال آخر: 5/8 + 2/8 = (5+2)/8 = 7/8
وفي هذه الحالة لا حاجة لتوحيد المقامات لأن المقام بالفعل متساوٍ. بعد الجمع، إذا كان الناتج كسرًا غير حقيقي، يمكن تحويله إلى عدد كسري.
الحالة الثانية: جمع كسور ذات مقامات مختلفة
إذا كانت الكسور التي نريد جمعها لها مقامات مختلفة، نبدأ أولًا بتوحيد المقامات. ويتم توحيد المقامات عن طريق إيجاد ما يُعرف باسم “المضاعف المشترك الأصغر” بين المقامين.
مثال: ½ + ⅓
نبحث عن مضاعف مشترك بين 2 و3، وأصغر عدد يقبل القسمة عليهما هو 6.
نحوّل الكسرين إلى مقامين متساويين:
½ = 3/6
⅓ = 2/6
الآن نجمع: 3/6 + 2/6 = 5/6
خطوات أساسية:
- تحديد المقام المشترك الأدنى (المضاعف المشترك الأصغر).
- تحويل كل كسر إلى كسر مكافئ له نفس المقام.
- جمع البسطين والإبقاء على المقام كما هو.
- تبسيط الناتج إن أمكن، أو تحويله إلى عدد كسري إذا كان غير حقيقي.
الحالة الثالثة: جمع الأعداد الكسرية المكوّنة من أعداد صحيحة وكسور
عندما نقوم بجمع أعداد كسرية على شكل عدد صحيح + كسر، فإننا نتبع القواعد نفسها، ولكن نُجمع الأعداد الصحيحة على حدة والكسور على حدة.
مثال: 1 ½ + 2 ⅓
أولًا: نجمع الأعداد الصحيحة: 1 + 2 = 3
ثم نجمع الكسور: ½ + ⅓ = 3/6 + 2/6 = 5/6
النتيجة = 3 5/6
تبسيط الكسور والنتائج
بعد جمع الكسور، من الأفضل دائمًا تبسيط النتيجة إن أمكن ذلك، لتكون الصورة أوضح وأسهل في الفهم. يمكن تبسيط الكسر بقسمة البسط والمقام على القاسم المشترك الأكبر.
مثال: 6/12 = ½ (لأن 6 ÷ 6 = 1 و12 ÷ 6 = 2)
تمارين تطبيقية على جمع الأعداد الكسرية
السؤال 1:
أوجد ناتج الجمع: 2/5 + 1/5
الحل: المقام نفسه، نجمع البسطين فقط: 2 + 1 = 3 → الناتج = 3/5
السؤال 2:
أوجد ناتج الجمع: ⅔ + ¾
الحل: توحيد المقامات: المقام المشترك الأدنى = 12
⅔ = 8/12
¾ = 9/12
المجموع: 8/12 + 9/12 = 17/12 = 1 5/12
السؤال 3:
أوجد ناتج الجمع: 1 ¼ + 2 ⅔
الحل: الأعداد الصحيحة: 1 + 2 = 3
الكسور: ¼ + ⅔ = 3/12 + 8/12 = 11/12
النتيجة النهائية = 3 11/12
أهمية تعلم جمع الأعداد الكسرية
تعلم جمع الأعداد الكسرية يُعد أساسًا لفهم مفاهيم رياضية أكثر تقدمًا مثل طرح الكسور، الضرب، القسمة، والمعادلات الجبرية في المستقبل. كما أنه يعتبر مهارة حيوية تساعد في التعرف إلى العلاقة بين الأجزاء والكل، والتمييز بين القيمة الكسرية والنسبية للأرقام، وفهم المكونات الدقيقة في الإفصاح عن الكميات.
إضافة إلى ذلك، يُستخدم هذا المفهوم في الحياة اليومية، ابتداءً من الطهي كما أسلفنا ذكره، وحتى في تنظيم الجدول اليومي، كأن تحدد كم ساعة خصصت للدراسة أو اللعب من أصل اليوم الكامل.
أخطاء شائعة يجب تجنبها
هناك بعض الأخطاء الشائعة التي يقع فيها الطلاب عند جمع الأعداد الكسرية، من أهمها:
- جمع المقامات عند جمع الكسور، وهو خطأ شائع. يجب فقط جمع البسط وترك المقام كما هو بعد توحيده.
- عدم تحويل الأعداد غير الحقيقية إلى أعداد كسرية إذا دعت الحاجة إلى ذلك.
- نسيان تبسيط الكسر النهائي، مما يترك الإجابة في صورة غير مُبسطة.
نصائح لتعلم الجمع الكسري بشكل أفضل
- التدرب المستمر على مسائل متنوعة.
- تمييز الفرق بين البسط والمقام بوضوح.
- استخدام النماذج والأشكال المرئية لتوضيح الكسور (مثل تقسيم الدوائر أو المربعات).
- الاعتماد على الجداول لتحديد المضاعف المشترك الأصغر بين المقامات.
هذه النصائح والتقنيات تسهّل العملية الحسابية وتقرب المفهوم إلى الذهن خاصة للطلبة الصغار.
المراجع
- وزارة التعليم – منهج الرياضيات للمرحلة الابتدائية، الطبعة المعتمدة 2023
- كتاب “الرياضيات الممتعة للأطفال”، دار المعرفة للنشر، 2021
- موقع BBC Bitesize – قسم الرياضيات للأطفال
- موقع Khan Academy – دروس الكسور والأعداد الكسرية
- National Council of Teachers of Mathematics (NCTM) Resources