الكسور هي جزء لا يتجزأ من عالم الرياضيات، وهي من المواضيع الأساسية التي يتعلمها طلاب المرحلة الابتدائية. تُستخدم الكسور في التعبير عن الأجزاء المنقسمة من الكل، وهي ضرورية لفهم العديد من المفاهيم الرياضية الأخرى، مثل النسب المئوية، القسمة، والقياس. تعلُّم الكسور يساعد الأطفال على بناء قاعدة قوية في التفكير المنطقي وحل المشكلات، كما أن لها تطبيقات يومية مهمة مثل الطهي، قراءة الوقت، ومقارنة الكميات.
ما هي الكسور؟
الكسر هو تعبير يُستخدم لتمثيل جزء من كل. يتكون الكسر من رقمين يُفصل بينهما خط أفقي أو مائل. الرقم العلوي يسمى البسط، ويمثل عدد الأجزاء التي نأخذها أو نشير إليها، بينما الرقم السفلي يسمى المقام ويمثل عدد الأجزاء المتساوية التي تم تقسيم الكل إليها.
مثال: في الكسر ٣/٤، الرقم ٣ هو البسط و٤ هو المقام، ما يعني أننا نأخذ ٣ أجزاء من أصل ٤ أجزاء متساوية.
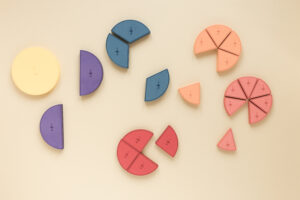
أنواع الكسور
1. الكسور الحقيقية
هي الكسور التي يكون فيها البسط أصغر من المقام، مثل: ١/٢، ٣/٥، ٤/٧. وتشير هذه الكسور إلى أقل من واحد صحيح.
2. الكسور غير الحقيقية
هي الكسور التي يكون فيها البسط أكبر من أو يساوي المقام، مثل: ٥/٤، ٧/٧، ٩/٨. هذه الكسور تشير إلى عدد أكبر من أو يساوي واحد صحيح.
3. الكسور المركبة
هي الجمع بين عدد صحيح وكسر حقيقي، وتُكتب بهذا الشكل: ١ ٣/٤، أي أن هناك واحد صحيح و٣/٤ كسر.
4. الكسور المتكافئة
هي الكسور التي على الرغم من اختلاف أرقامها، إلا أنها تمثل نفس الجزء من الكل. على سبيل المثال، ١/٢ و٢/٤ و٤/٨ كلها متكافئة لأنها تمثل نفس القيمة.
5. الكسور العشرية
هي الكسور التي يتم التعبير عنها باستخدام الفاصلة العشرية بدلاً من الكسر التقليدي. على سبيل المثال، ٠٫٥ يعادل ١/٢.
تمثيل الكسور بصريًا
لفهم الكسور بشكل أوضح، يتم استخدام التمثيل البصري مثل تقسيم الأشكال الهندسية. على سبيل المثال، يمكن تقسيم دائرة إلى أربعة أقسام متساوية، وتلوين ثلاثة منها لتوضيح الكسر ٣/٤. هذا النوع من التمثيل يساعد الطلاب على تصور ما تعنيه الكسور بالضبط، ويجعل تعلمها أكثر سهولة ومتعة.
قواعد مهمة عند التعامل مع الكسور
1. تبسيط الكسور
يعني تبسيط الكسر تحويله إلى أبسط صورة له بواسطة قسمة البسط والمقام على أكبر عامل مشترك بينهما. مثال: الكسر ٦/٨ يمكن تبسيطه إلى ٣/٤ بعد قسمة البسط والمقام على ٢.
2. توحيد المقامات
لتتمكن من جمع أو طرح الكسور ذات المقامات المختلفة، يجب أولاً توحيد المقامات. يتم ذلك عن طريق إيجاد المقام المشترك الأصغر، وتحويل الكسور إليه. مثال: لجمع ١/٣ و١/٤، يمكن توحيد المقامات إلى ١٢، ثم تحويل الكسور: ٤/١٢ + ٣/١٢ = ٧/١٢.
3. مقارنة الكسور
يمكن مقارنة الكسور بتوحيد مقاماتها أو بتحويلها إلى أعداد عشرية. على سبيل المثال، للمقارنة بين ٢/٣ و٣/٥، يمكن توحيد المقامات أو تحويلهما إلى ٠٫٦٦ و٠٫٦ لمعرفة أن ٢/٣ أكبر.
العمليات الأربع على الكسور
الجمع
تُجمع الكسور بتوحيد المقامات ثم جمع البسوط. مثال: ١/٤ + ٢/٤ = ٣/٤. وإذا لم تكن المقامات موحدة، نبدأ بتوحيد المقامات. مثال: ١/٢ + ١/٣ = ٣/٦ + ٢/٦ = ٥/٦.
الطرح
تشبه عملية الطرح الجمع، حيث يتم توحيد المقامات أولاً إن لزم الأمر، ثم نطرح البسطين. مثال: ٣/٥ – ١/٥ = ٢/٥. أو: ٥/٦ – ١/٣ = ٥/٦ – ٢/٦ = ٣/٦ = ١/٢ بعد التبسيط.
الضرب
ضرب الكسور بسيط، نضرب البسط في البسط والمقام في المقام. مثال: ٢/٣ × ٣/٤ = ٦/١٢ = ١/٢ بعد التبسيط.
القسمة
لقسمة الكسور، نُبدل الكسر الثاني (المقسوم عليه) إلى مقلوبه ثم نضرب. مثال: ٢/٣ ÷ ٤/٥ = ٢/٣ × ٥/٤ = ١٠/١٢ = ٥/٦ بعد التبسيط.
الكسور في الحياة اليومية
الكسور ليست فقط في الكتب المدرسية! نحن نستخدم الكسور باستمرار في حياتنا – عند قياس المكونات في الطبخ، عند تقسيم وقت اللعب، أو حتى عند مشاركة الطعام بين الأصدقاء. على سبيل المثال، إذا أردت تقطيع بيتزا إلى ٨ قطع ووزعتها على ٤ أشخاص، فإن كل شخص يحصل على ٢/٨ أو ١/٤ من البيتزا.
هل تعلم؟ يستخدم الطيارون الكسور عند حساب كمية الوقود، بحيث يحددون إن كان لديهم ٣/٤ من الخزان ممتلئاً، مما يساعدهم على تحديد مدى الرحلة!
تطبيقات على الكسور من واقع الحياة
في الطبخ، تقرأ المقادير بكسور مثل ١/٢ كوب من السكر أو ٣/٤ ملعقة من الملح. في هذه الحالة، من المهم معرفة الحجم الكلي للمقدار ثم معرفة كيف تقيس الجزء المطلوب.
في الرياضة، تُستخدم الكسور لتحديد نسبة الإنجاز. فإذا أحرز فريق ما ٥ أهداف من أصل ٨ فرص، فإن نسبة النجاح هي ٥/٨.
وفي المدرسة، إذا أجاب الطالب على ٧ من أصل ١٠ أسئلة بشكل صحيح، فإن النتيجة تكون ٧/١٠، والتي تُمثل ٧٠٪ عند تحويلها إلى نسبة مئوية.
أخطاء شائعة في فهم الكسور
من الأخطاء التي يقع فيها الطلاب اعتقادهم بأن الكسر ذو المقام الأكبر هو الأكبر، مثلاً يفترض البعض أن ١/٨ أكبر من ١/٤ لأن الرقم ٨ أكبر من ٤، ولكن في الكسور، كلما كبر المقام، كلما صغر الجزء. لذا ١/٨ أصغر من ١/٤.
خطأ آخر هو عند المقارنة بين الكسور ومقارنتها بشكل غير صحيح دون توحيد المقامات. يجب دائمًا التفكير في أن الكسر يعبّر عن جزء من وحدة كاملة، لذا التصوّر البصري مهم جداً لفهم الكسور على نحو صحيح.
أنشطة واقتراحات لتعلم الكسور بطريقة ممتعة
لتسهيل فهم الكسور، يمكن للمعلمين وأولياء الأمور إجراء أنشطة تفاعلية، مثل:
- تقطيع أشكال الطعام (بيتزا، فطائر، شوكولاتة) إلى أجزاء مختلفة، وطلب نسبتها بالكسر.
- الرسم باستخدام الألوان لتمثيل الكسور على مربعات أو دوائر مقسمة.
- ألعاب البطاقات التي تحتوي على كسور ومطلوب مطابقة الكسور المتكافئة.
الأساليب الحسية والحركية تساعد الطالب على تذكر مفهوم الكسر بسهولة، وتحول التعلم إلى تجربة ممتعة.
تحديات واستعداد للمرحلة الإعدادية
عند اقتراب الطلاب من نهاية المرحلة الابتدائية، من المهم أن يكونوا قادرين على إجراء العمليات الأربع على الكسور بدقة، وفهم كيفية تحويل الكسور إلى أعداد عشرية وعكسها. كما يجب عليهم القدرة على تطبيق الكسور في مسائل حياتية وحلول تطبيقية. هذه المهارات تشكل الأساس لفهم النسب والمعدلات وإجراء العمليات الجبرية في المراحل التعليمية التالية.
مراجعة عامة
تعلم الكسور جزء أساسي ومهم في الرياضيات للمرحلة الابتدائية، ويهيئ الطفل لفهم أكثر عمقًا للمفاهيم الرياضية القادمة. باستخدام التمثيل البصري، والأمثلة الواقعية، والتطبيقات العملية، يمكن للطالب أن يكتسب فهمًا شاملًا للكسور، ويصبح مستعدًا للانتقال إلى النسب المئوية، الأعداد العشرية، والمعادلات الجبرية في المستقبل.
قائمة المراجع
- وزارة التعليم، كتاب الرياضيات للمرحلة الابتدائية – الصف الرابع والخامس والسادس.
- National Council of Teachers of Mathematics – Fractions and Decimals (NCTM.org).
- BBC Bitesize – Maths: Understanding Fractions.
- Math is Fun – Fractions for Kids (www.mathsisfun.com).
- جمعية الرياضيات المصرية، دليل المدرّس لمادة الرياضيات في المرحلة الابتدائية.






